Graphing with Excel

Linear Regression in Excel

Table of Contents

1. Create an initial scatter plot
2. Creating a linear regression line (trendline)
3. Using the regression equation to calculate slope and intercept
4. Using the R-squared coefficient calculation to estimate fit

Introduction

Regression lines can be used as a way of visually depicting the relationship between the independent (x) and dependent (y) variables in the graph. A straight line depicts a linear trend in the data (i.e., the equation describing the line is of first order. For example, y = 3x + 4. There are no squared or cubed variables in this equation). A curved line represents a trend described by a higher order equation (e.g., y = 2x² + 5x - 8). It is important that you are able to defend your use of either a straight or curved regression line. That is, the theory underlying your lab should indicate whether the relationship of the independent and dependent variables should be linear or non-linear.

In addition to visually depicting the trend in the data with a regression line, you can also calculate the equation of the regression line. This equation can either be seen in a dialogue box and/or shown on your graph. How well this equation describes the data (the 'fit'), is expressed as a correlation coefficient, R² (R-squared). The closer R² is to 1.00, the better the fit. This too can be calculated and displayed in the graph.

The data below was first introduced in the basic graphing module and is from a chemistry lab investigating light absorption by solutions. Beer's Law states that there is a linear relationship between concentration of a colored compound in solution and the light absorption of the solution. This fact can be used to calculate the concentration of unknown solutions, given their absorption readings. This is done by fitting a linear regression line to the collected data.

Creating an initial scatter plot

Before you can create a regression line, a graph must be produced from the data. Traditionally, this would be a scatter plot. This module will start with the scatter plot created in the basic graphing module.

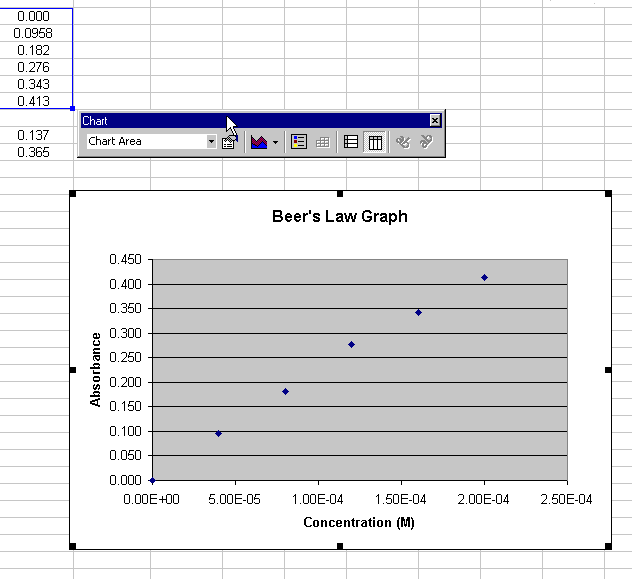
Figure 1.

Return to Top

Creating a Linear Regression Line (Trendline)

When the chart window is highlighted, you can add a regression line to the chart by choosing Chart > Add trendline...

A dialogue box appears (Figure 2). Select the Linear Trend/Regression type:

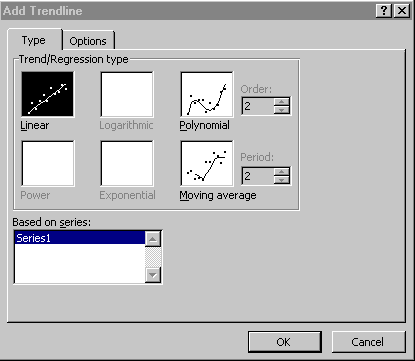
Figure 2.

Choose the Options tab and select Display equation on chart (Figure 3):

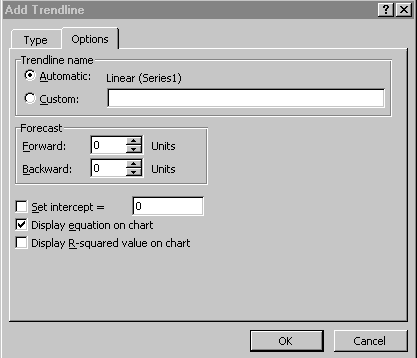
Figure 3.

Click OK to close the dialogue. The chart now displays the regression line (Figure 4)

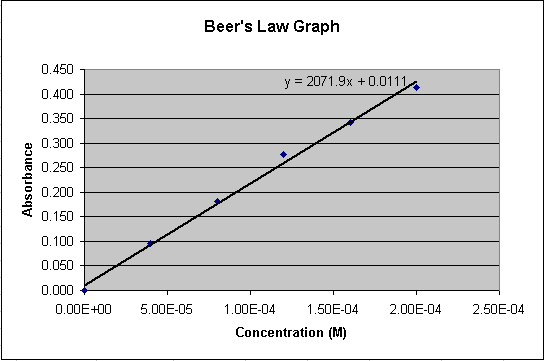
Figure 4.

Return to Top

Using the Regression Equation to Calculate Concentrations

The linear equation shown on the chart represents the relationship between Concentration (x) and Absorbance (y) for the compound in solution. The regression line can be considered an acceptable estimation of the true relationship between concentration and absorbance. We have been given the absorbance readings for two solutions of unknown concentration.

Using the linear equation (labeled A in Figure 5), a spreadsheet cell can have an equation associated with it to do the calculation for us. We have a value for y (Absorbance) and need to solve for x (Concentration). Below are the algebraic equations working out this calculation:

y = 2071.9x + 0.111

y - 0.0111 = 2071.9x

(y - 0.0111) / 2071.9 = x

Now we have to convert this final equation into an equation in a spreadsheet cell. The equation associated with the spreadsheet cell will look like what is labeled C in Figure 8. 'B12' in the equation represents y (the absorbance of the unknown). The solution for x (Concentration) is then displayed in cell 'C12'.

• Highlight a spreadsheet cell to hold 'x', the result of the final equation (cell C12, labeled B in Figure 5).
• Click in the equation area (labeled C, figure 5)
• Type an equal sign and then a parentheses
• Click in the cell representing 'y' in your equation (cell B12 in Figure 5) to put this cell label in your equation
• Finish typing your equation

Note: If your equation differs for the one in this example, use your equation

Duplicate your equation for the other unknown.

• Highlight the original equation cell (C12 in Figure 5) and the cell below it (C13)
• Choose Edit > Fill > Down

Return to Top

Note that if you highlight your new equation in C13, the reference to cell B12 has also incremented to cell B13.

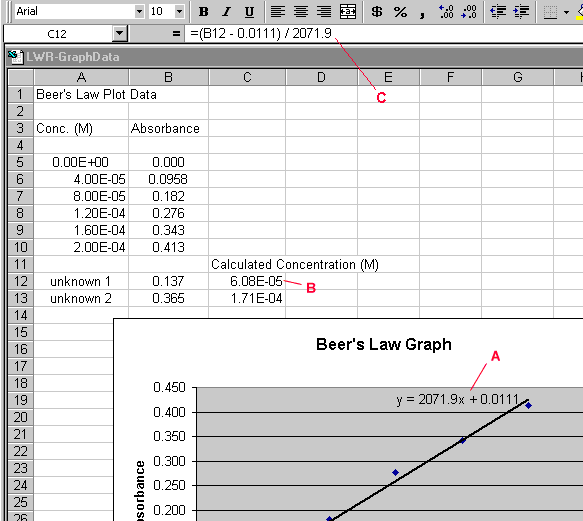
Figure 5.

Return to Top

Using the R-squared coefficient calculation to estimate fit

Double-click on the trendline, choose the Options tab in the Format Trendlines dialogue box, and check the Display r-squared value on chart box. Your graph should now look like Figure 6. Note the value of R-squared on the graph. The closer to 1.0, the better the fit of the regression line. That is, the closer the line passes through all of the points.

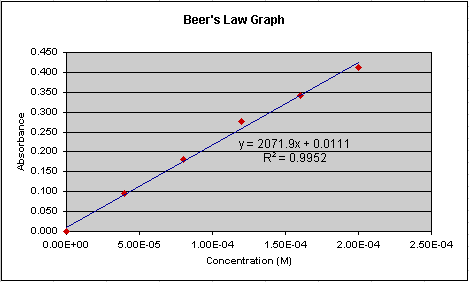
Figure 6.

Now lets look at another set of data done for this lab (Figure 7). Notice that the equation for the regression line is different than is was in Figure 6. A different equation would calculate a different concentration for the two unknowns. Which regression line better represents the 'true' relationship between absorption and concentration? Look at how closely the regression line passes through the points in Figure 7. Does it seem to 'fit' as well as it does in Figure 6? No, and the R-squared value confirms this. It is 0.873 in Figure 7 compared to 0.995 in Figure 6. Though we would need to take in to account information such as the number of data points collected to make an accurate statistical prediction as to how well the regression line represents the true relationship, we can generally say that Figure 6 represents a better representation of the relationship of absorption and concentration.

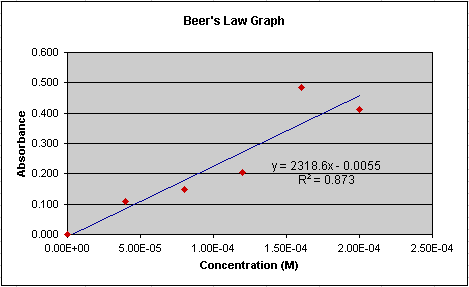
Figure 7.

Return to Top